Mathematik – Aha 2 – Lösung
Erdgürtel – Lösung
Erstaunlicherweise würde sich das Seil (falls man dies überhaupt bewerkstelligen könnte) um fast 16cm vom Boden abheben, wie die folgende Rechnung zeigt.
Man hebt das Seil überall um x vom Boden und erhält einen Kreis mit Radius r + x, wobei r den Erdradius darstellt. Der Umfang dieses etwas größeren Kreises beträgt 40 000 km + 1m, also gleich 2 π r + 1m.
Die Umformung zeigt, dass sich der Term 2 π r weghebt und x nur noch von der Verlängerung 1m abhängt.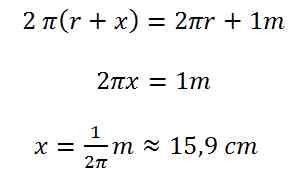
Es ist also egal, wie groß der Kreis ist, dessem Umfang man um einen Meter verlängert. Die Radiusänderung beträgt immer 15,9 cm.
Dies ist der Radius eines Kreises mit Umfang 1 m.
Etwas besser vorstellen kann man sich das ganze, wenn man folgendes Gedankenexperiment macht:
Man baut um die ganze Erde einen Steg mit 15,9cm Höhe über dem Boden. Zwei Personen laufen nebeneinander um die ganze Welt, die eine auf dem Boden, die andere auf dem Steg. Die Personen laufen fast genau gleich weit. Die Person auf dem Steg läuft ja immer genau neben der anderen.Insgesamt addiert sich der winzige Unterschied nach einer Erdumrundung auf einen Meter.
